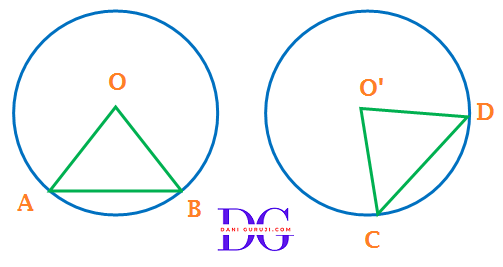KEY Concept For Chpt. 9.1 Circles
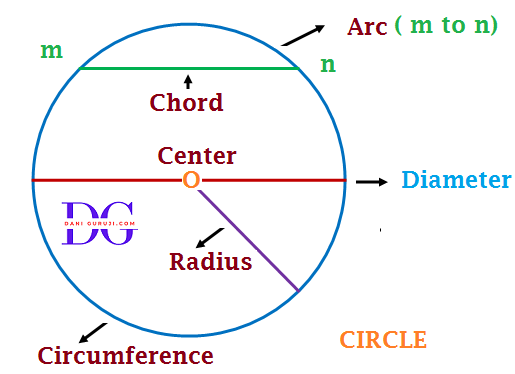
Circle
A circle is the collection of all points, which are equidistant from a fixed point in the plane.
Radius
Any line segment starting at the centre of the circle and joining anywhere on the border on the circle is a Radius of Circle.
Chord
Any line segment that’s both endpoints (starting and ending) anywhere on the border on the circle is known as Chord .
Diameter
The longest chord of a circle and which passes through the centre of the Circle is a Diameter of the circle.
Arc
An arc is a smooth curve joining two points anywhere on the border on the circle . A continuous piece of a circle is Arc of the circle .
Circumference
It is the length of the circle if we open and straightened out to make a line segment.
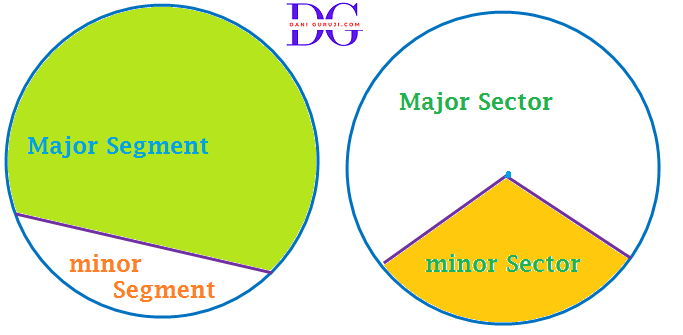
Segment
The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle. It could be a major or minor segment.
Sector
The region between an arc and the two radii, joining the centre to the end points of the arc is called a sector. It could be a major or minor sector.
Theorem 9.1
Equal chords of a circle subtend equal angles at the centre.
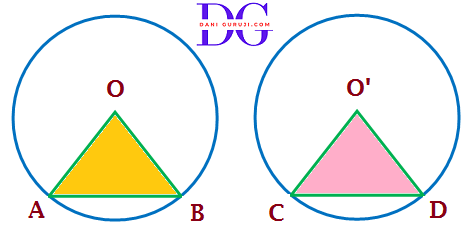
Theorem 9.2
If the angles subtend by two chords of a circle at the centre ( corresponding centers ) are equal, then the chords must be equal.